Prolog Übung
zur Vorlesung Logik in der Informatik
Aktuelles
Abgabehinweise
Abgabehinweise für die -digitale- Abgabe der Prolog-Übungsaufgaben über moodle (ab Übungsblatt 3).
Die Abgabe der Datei mit dem Prolog-Quellcode muss den Namen blattx.pl tragen, wobei x durch die aktuelle Blattnummer ersetzt wird. So sollte die Datei für die Abgabe von Aufgabe 4 von Blatt 3 den Namen blatt3.pl tragen.
In jeder Abgabe soll das Prädikat matnr/1 exakt für Ihre Matrikelnummer gelten. Wenn Sie also die Matrikelnummer 123456 haben, soll Prolog auf die Anfrage ?- matnr(X). mit X = 123456. antworten. Wird die Datei über einen moodle-Account abgegeben, werden frühere Abgaben für diese Aufgabe überschrieben.
Beachten Sie, dass wir Ihre Bearbeitung dieser Aufgaben nur dann bewerten, wenn sich der abgegebene Prolog-Quellcode von SWI-Prolog auf gruenau6 ohne Fehlermeldungen laden lässt und die Abarbeitung gegebener Beispielanfragen nicht länger als 10 Sekunden dauert!
Korrekturanmerkungen zu Ihren Prolog-Abgaben können in Moodle unter Bewertungen (in der Navigationsleiste) eingesehen werden.
Downloads
Hier finden Sie zu gegebener Zeit die für die Lösung einzelner Aufgaben benötigten Dateien:
- Die für Blatt 7 (und folgende) benötigte Datei al.pl
- Die für Blatt 9 benötigte Datei kinodb.pl
- Die für Blatt 10 benötigte Dateien al_def.pl, al_literals.pl und al_nf.pl
- Übungsblatt 11: die Module pure_literal und unit_propagation.
- Übungsblatt 13: die Module tseitin und dpll.
Weiterhin finden Sie nachfolgend Probleminstanzen für SAT-Solver im DIMACS-Format. Wer mehr zu den Beispielen 2--x wissen möchte, kann sich unter http://massimolauria.net/cnfgen/ über die Herkunft der Formeln informieren. Ich habe einige Instanzen mal auf gruenau6 mit unserer Implementation laufen lassen und man kann sehr gut ablesen, wie sich unser Solver so mit steigendem n klarkommt... (Speichern durch Anklicken des Dateinamens)
| Name der Datei | benötigte Zeit in Sekunden | Anzahl der Ableitungen | |
| Beispiel 2.64 der VL | VLBeispiel264.cnf | 0.002 seconds | 2,814 inferences |
| Pebbling formula of: Pyramid of height n |
pyramid10.cnf | 0.008 seconds | 28,386 inferences |
| pyramid15.cnf | 0.029 seconds | 110,095 inferences | |
| pyramid50.cnf | 1.631 seconds | 9,668,024 inferences | |
| Pigeonhole principle formula for n+1 pigeons and n holes |
php4_3.cnf | 0.003 seconds | 10,439 inferences |
| php5_4.cnf | 0.010 seconds | 64,762 inferences | |
| php6_5.cnf | 0.085 seconds | 406,535 inferences | |
| php7_6.cnf | 0.489 seconds | 2,691,573 inferences | |
| php8_7.cnf | 2.878 seconds | 19,514,171 inferences | |
| php9_8.cnf | 22.321 seconds | 157,722,886 inferences | |
| php10_9.cnf | 166.006 seconds | 1,423,024,293 inferences | |
| php11_10.cnf | 2124.783 seconds | 14,237,397,770 inferences | |
| php12_11.cnf | 22926.179 seconds ~6h22 | 156,624,865,223 inferences | |
| php13_12.cnf | 275571.056 seconds ~3T4h33 | 1,879,522,854,956 inferences | |
| php14_13.cnf | ... | .. | |
| php15_14.cnf | ... | .. |
Zur Info: aktuelle SAT-Solver brechen auch ab php13_12 ein.
Beispiele aus der Übung
Woche 01 · Woche 02· Woche 03· Woche 04· Woche 05· Woche 06· Woche 07· Woche 08· Woche 09· Woche 10· Woche 11
Definition eines Suchbaumes:
Ein Suchbaum der Anfrage A über der Wissensbasis WB ist eine Erweiterung eines geordneten Baums dessen Knoten und Kanten Beschriftungen tragen können mit den folgenden Eigenschaften:
- Die Wurzel ist mit A gekennzeichnet.
- Alle Knoten sind mit einer Anfrage beschriftet, insbesondere enthalten Blätter entweder die leere Anfrage oder sind zusätzlich unterhalb der Blätter mit † gekennzeichnet.
- Ein Blatt ist genau dann zusätzlich mit † gekennzeichnet, falls der erste Term der Anfrage (Beschriftung des Blattes) mit keinem Kopf irgendeiner Regel (bzw. Fakt) aus WB unifiziert werden kann.
- Ist Knoten v ein Kindknoten von Knoten w, dann
- ) existiert eine Regel r in WB, so dass der erste Term der Anfrage (Beschriftung von w) sich mit dem Kopf von r unifizieren läßt.
- ) Sei r' eine Regel, entstanden aus r, bei der alle Variablen so umbenannt sind, dass sie nicht in der Anfrage vorkommen.
- ) Sei S die Menge der Variableninstanziierungen bei der Unifikation des Kopfes von r' mit dem ersten Term der Anfrage (von w).
- ) Die Beschriftung von v entsteht durch Ersetzen des ersten Terms der Anfrage von w durch den Körper der umbenannten Regel r' und der Ersetzung von Variablen entsprechend S.
- ) Die Instanziierungen der Variablen des ersetzten Terms der Anfrage stehen an der Kante von w nach v.
- Knoten v mit Beschriftung A besitzt für jede Regel r, deren Kopf sich mit dem ersten Term der Anfrage A unifizieren läßt, einen Kindknoten. Die Reihenfolge der Kindknoten, wird durch die Reihenfolge der Vorkommen der angewendeten Regeln in WB bestimmt.
Woche 01
geld_verbrannt.
lachgas.
woman(jody).
woman(yolanda).
loves(vincent, mia).
loves(marsellus, mia).
playsAirGuitar(jody).
party.
loves(ramona,todd).
time_flies(_).
ramonasEvilExes(lucas).
ramonasEvilExes(X) :- time_flies(X), loves(ramona,X).
fights(knives,X):-loves(X,scott).
fights(scott,X):- ramonasEvilExes(X).
loves(ramona,roxy).
loves(ramona,todd).
time_flies(_).
ramonasEvilExes(lucas).
ramonasEvilExes(X) :- time_flies(X), loves(ramona,X).
fights(knives,X):-loves(X,scott).
fights(scott,X):- ramonasEvilExes(X).
Woche 02
loves(mia,X) :- good_dancer(X).
kills(marsellus,X) :- loves(mia,X).
f(b).
g(a).
g(b).
h(b).
k(X) :- f(X), g(X), h(X).
Programmieren mit Unifikation:

Aufgabe 2.4 aus [BBS]
Die Worte werden dabei wie folgt in der Wissensbasis repräsentiert:
word(astoria, a,s,t,o,r,i,a).
word(baratto, b,a,r,a,t,t,o).
word(cobalto, c,o,b,a,l,t,o).
word(pistola, p,i,s,t,o,l,a).
word(statale, s,t,a,t,a,l,e).
Programmieren mit Nicht-Unifizierbarkeit:
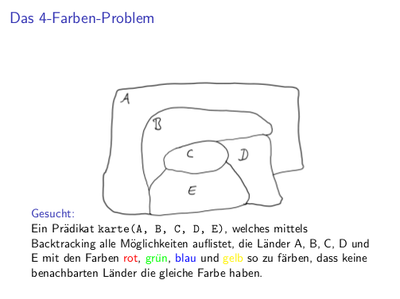
Woche 03
kind(brigitte, carolin).
kind(carolin, donna).
kind(donna, emilie).
nachkomme(X, Y) :- kind(X, Y).
nachkomme(X, Y) :- kind(X, Z), nachkomme(Z, Y).
kind(brigitte, carolin).
kind(carolin, donna).
kind(donna, emilie).
nachkomme(X, Y) :- kind(X, Z), nachkomme(Z, Y).
nachkomme(X, Y) :- kind(X, Y).
kind(brigitte, carolin).
kind(carolin, donna).
kind(donna, emilie).
nachkomme(X, Y) :- nachkomme(Z, Y), kind(X, Z).
nachkomme(X, Y) :- kind(X, Y).
kind(brigitte, carolin).
kind(carolin, donna).
kind(donna, emilie).
nachkomme(X, Y) :- kind(X, Y).
nachkomme(X, Y) :- nachkomme(Z, Y), kind(X, Z).
numeral(succ(X)) :- numeral(X).
double(succ(X),succ(succ(Y))) :- double(X,Y).
add(0,Y,Y).
add(succ(X),Y,succ(Z)):- add(X,Y,Z).
offen:
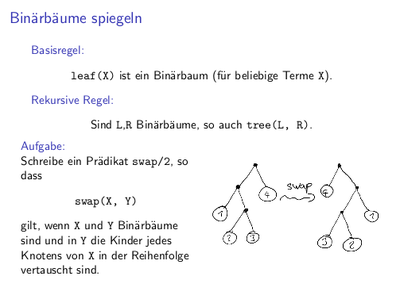
Woche 04
element(X,[_|T]) :- element(X,T).
invert([a|T1],[b|T2]) :- invert(T1,T2).
invert([b|T1],[a|T2]) :- invert(T1,T2).
evenElements([], []).
evenElements([_, X|T1], [X|T2]) :- evenElements(T1,T2).
Woche 05
laenge([_|T],L) :- laenge(T,LT),L is LT + 1.
laenge([_|T],A,N) :- AT is A + 1 , laenge(T,AT,N).
laenge(L, N) :- laenge(L,0,N).
prod([], A, A).
prod([H|T], A, P) :- A2 is A * H, prod(T, A2, P).
max([H|T], A, MT) :- H > A, max(T, H, MT).
max([H|T], A, MT) :- H =< A, max(T, A, MT).
max([H|T], M) :- max(T, H, M).
Offen: Der Klassiker der Rekursion
Die Fakultät n! einer natürlichen Zahl n ist definiert durch:

Definieren Sie
- ein Prädikat fak/2, dass bei Anfrage fak(X,Y) die Fakultät von X mit Y unifiziert.
- ein Prädikat fakAcc/2, dass äquivalent zu fak/2 ist und "End-Rekursiv” realisiert.
Woche 06
verkettet([], Y, Y).
verkettet([H|T], Y, [H|T2]) :- verkettet(T, Y, T2).
% praefix
praefix(X, Y) :- verkettet(X, _, Y).
% suffix
suffix(X, Y) :- verkettet(_, X, Y).
umgedreht([], []).
umgedreht([H|T], R) :-
umgedreht(T, RT), verkettet(RT, [H], R).
% mit Akkumulator
umgedrehtAcc([], A, A).
umgedrehtAcc([H|T], A, R) :-
umgedrehtAcc(T, [H|A], R).
umgedrehtAcc(L, R) :- umgedrehtAcc(L, [], R).
% verkettet
verkettet([], Y, Y).
verkettet([H|T], Y, [H|T2]) :- verkettet(T, Y, T2).
not_member(X, [H|T]) :- X \= H, not_member(X, T).
atree(tree(L, R)) :- atree(L), atree(R).
sum_labels(tree(L, R), N) :-
sum_labels(L, NL), sum_labels(R, NR),
N is NL + NR.
lookup(X,[_|T],Y) :- lookup(X,T,Y).
node(f). node(g). node(h). node(i). node(j).
edge(a, j).
edge(c, e).
edge(d, e).
edge(e, f).
edge(f, g).
edge(g, h). edge(g, j).
edge(h, g). edge(h, i).
edge(i, a). edge(i, b). edge(i, j).
edge(j, b). edge(j, c). edge(j, d). edge(j, f).
erreichbar(X, X).
erreichbar(X, Y) :-
edge(X, Z), erreichbar(Z, Y).
% Try: ?- erreichbar(a, g).
% Try: ?- erreichbar(h, a).
node(f). node(g). node(h). node(i). node(j).
edge(a, j).
edge(c, e).
edge(d, e).
edge(e, f).
edge(f, g).
edge(g, h). edge(g, j).
edge(h, g). edge(h, i).
edge(i, a). edge(i, b). edge(i, j).
edge(j, b). edge(j, c). edge(j, d). edge(j, f).
erreichbarMem(X, Y) :- erreichbar(X, Y, [X]).
erreichbar(X, X, _) .
erreichbar(X, Y, Pfad) :-
edge(X, Z), not_member(Z, Pfad),
erreichbar(Z, Y, [Z|Pfad]).
% Try: ?- erreichbarMem(a, g).
% Try: ?- erreichbarMem(h, a).
% not_member
not_member(_, []).
not_member(X, [H|T]) :- X \= H, not_member(X, T).
Woche 07
distribute((A + B)*C, A*C + B*C).
numbers(L + R, X) :-
numbers(L, XL), numbers(R, XR),
append(XL, XR, X).
numbers(L * R, X) :-
numbers(L, XL), numbers(R, XR),
append(XL, XR, X).
atom_codes(N, SN),
atom_codes("x", XN),
append(XN, SN, S),
atom_codes(A, S).
Woche 08
s(0, 0).
q(X, Y) :- i(X), i(Y).
q(3, 3).
i(1).
i(2).
s(0, 0).
q(X, Y) :- i(X), !, i(Y).
q(3, 3).
i(1).
i(2).
max(X, Y, X) :- X > Y.
max(X, Y, X) :- X > Y.
max(X, _, X).
% Try
%
% ?-max(2,3,X).
%
% ?- max(3,2,X).
%
% ?- max(2,3,2).
max(X, _, X).
mag(etienne,X) :- schule(X).
schule(X) :- fach1(X).
schule(X) :- fach2(X).
schule(X) :- non_fach(X).
non_fach(hofpause).
non_fach(mittagspause).
non_fach(kleine_pause).
fach1(sport).
fach1(musik).
fach1(kunst).
fach2(deutsch).
fach2(englisch).
neg(_).
schule(X) :- fach1(X).
schule(X) :- fach2(X).
schule(X) :- non_fach(X).
non_fach(hofpause).
non_fach(mittagspause).
non_fach(kleine_pause).
fach1(sport).
fach1(musik).
fach1(kunst).
fach2(deutsch).
fach2(englisch).
Woche 09
retract(sad(X)),
assert(happy(X)).
fak(0, 1).
fak(N, X) :- lookup(N, X), !.
fak(N, X) :- N > 0,
N2 is N - 1,
fak(N2, X2),
X is N * X2,
assert(lookup(N, X)).
child(charlotte, caroline).
child(caroline, laura).
child(laura, rose).
descend(X, Y) :- child(X, Y).
descend(X, Y) :- child(X, Z), descend(Z, Y).
% Try
%
% ?- descend(martha, X).
%
% ?- findall(X, descend(martha, X), L).
Woche 10
read(S, X),
\+ X = end_of_file, !,
summe(S, N2), N is N2 + X.
summe(_, 0).
printActors(F) :-
setof(S, R^film(F, R, S), L),
displayList(L).
displayList([]) :- nl.
displayList([X|L]) :-
write(X), tab(1), displayList(L).
% test:
% ?- printActors('Casablanca').
% Humphrey Bogart Ingrid Bergmann
% true.
printMovies(R) :-
setof(F, S^film(F, R, S),L),
displayList(L).
displayList([]) :- nl.
displayList([X|L]) :-
write(X), nl, displayList(L).
% test:
% ?- printMovies('Ridley Scott').
% Alien
% Blade Runner
Woche 11
np(Z) :- det(X), n(Y), append(X,Y,Z).
vp(Z) :- v(X), np(Y), append(X,Y,Z).
vp(Z) :- v(Z).
det([a]).
det([the]).
n([woman]).
n([man]).
v([shoots]).
np(Z) :- append(X,Y,Z), det(X), n(Y).
vp(Z) :- append(X,Y,Z), v(X), np(Y).
vp(Z) :- v(Z).
det([a]).
det([the]).
n([woman]).
n([man]).
v([shoots]).
np(X, Z) :- det(X, Y), n(Y, Z).
vp(X, Z) :- v(X, Y), np(Y, Z).
vp(X, Z) :- v(X, Z).
det([the|W], W).
det([a|W], W).
n([woman|W], W).
n([man|W], W).
v([shoots|W], W).
np --> det, n.
vp --> v, np.
vp --> v.
det --> [the].
det --> [a].
n --> [woman].
n --> [man].
v --> [shoots].
np --> det, ne.
ne --> n.
ne --> a, ne.
vp --> v, np.
det --> [the].
det --> [a].
n --> [dog].
n --> [bone].
n --> [mouse].
n --> [cat].
v --> [ate].
v --> [chases].
a --> [big].
a --> [brown].
a --> [lazy].
essen --> zutat.
zutat --> ['Kartoffeln'].
zutat --> ['Sahne'].
zutat --> ['Zwiebeln'].
zutat --> ['Schokoladenstreusel'].
essen --> essen, ['mit'], zutat.
zutat --> ['Kartoffeln'].
zutat --> ['Sahne'].
zutat --> ['Zwiebeln'].
zutat --> ['Schokoladenstreusel'].
s --> l, s, r.
l --> [a].
r --> [b].
Literatur
| [BBS] | Patrick Blackburn, Johan Bos, Kristina Striegnitz, Learn PROLOG Now!. Kings College Publications, 2006. Online version. |
Browser-ErweiterungMatthias Vogt hat eine Browser-Erweiterung für Chromium und Firefox veröffentlicht, welche der Online-Version von Learn PROLOG Now! ein moderneres Aussehen verleiht. Die Quellen sind auf GitHub verfügbar. |
|
| [SS] | Ehud Shapiro, Leon Sterling, The Art of PROLOG: Advanced Programming Techniques. 2nd Edition, MIT Press, 1994. |
Programmierresourcen
SWI-Prolog. Ein Kurzanleitung für den Einstieg in SWI-Prolog.

