Prolog Übung
zur Vorlesung Logik in der Informatik
Aktuelles
-
Beachten Sie: Für die Nutzung der Rechner der RBG in der Übung, wie auch für den Zugang des Referenzrechners, ist zwingend (seit diesem Semester) ein Informatik-Account notwendig (hier rechtzeitig beantragen). Ein Zugang mittels CMS-Account ist nicht mehr möglich.
- Die Prolog-Übung findet erstmalig in der zweiten Woche der Vorlesungszeit statt, also am 21.10.25 bzw. 23.10.25.
Abgabehinweise
Abgabehinweise für die -digitale- Abgabe der Prolog-Übungsaufgaben über moodle (ab Übungsblatt 3).
Die Abgabe der Datei mit dem Prolog-Quellcode muss den Namen blattx.pl tragen, wobei x durch die aktuelle Blattnummer ersetzt wird. So sollte die Datei für die Abgabe von Aufgabe 4 von Blatt 3 den Namen blatt3.pl tragen.
In jeder Abgabe soll das Prädikat matnr/1 exakt für Ihre Matrikelnummer gelten. Wenn Sie also die Matrikelnummer 123456 haben, soll Prolog auf die Anfrage ?- matnr(X). mit X = 123456. antworten. Wird die Datei über einen moodle-Account abgegeben, werden frühere Abgaben für diese Aufgabe überschrieben.
Beachten Sie, dass wir Ihre Bearbeitung dieser Aufgaben nur dann bewerten, wenn sich der abgegebene Prolog-Quellcode von SWI-Prolog auf gruenau6 ohne Fehlermeldungen laden lässt und die Abarbeitung gegebener Beispielanfragen nicht länger als 10 Sekunden dauert!
Korrekturanmerkungen zu Ihren Prolog-Abgaben können in Moodle unter Bewertungen (in der Navigationsleiste) eingesehen werden.
Eine Kurzanleitung für den Fernzugriff auf gruenau6 findet sich hier.
Downloads
Hier finden Sie zu gegebener Zeit die für die Lösung einzelner Aufgaben hilfreiche bzw. benötigten Dateien:
- Die in Aufgabenblatt 1 beschriebene Wissensbasis ring.pl
- Die in Aufgabenblatt 7 (und folgende) benötigte Datei al.pl
Beispiele aus der Übung
Woche 01
geld_verbrannt.
lachgas.
woman(jody).
woman(yolanda).
loves(vincent, mia).
loves(marsellus, mia).
playsAirGuitar(jody).
party.
loves(ramona,todd).
time_flies(_).
ramonasEvilExes(lucas).
ramonasEvilExes(X) :- time_flies(X), loves(ramona,X).
fights(knives,X):-loves(X,scott).
fights(scott,X):- ramonasEvilExes(X).
loves(ramona,roxy).
loves(ramona,todd).
time_flies(_).
ramonasEvilExes(lucas).
ramonasEvilExes(X) :- time_flies(X), loves(ramona,X).
fights(knives,X):-loves(X,scott).
fights(scott,X):- ramonasEvilExes(X).
Woche 02
loves(mia,X) :- good_dancer(X).
kills(marsellus,X) :- loves(mia,X).
f(b).
g(a).
g(b).
h(b).
k(X) :- f(X), g(X), h(X).
Programmieren mit Unifikation:
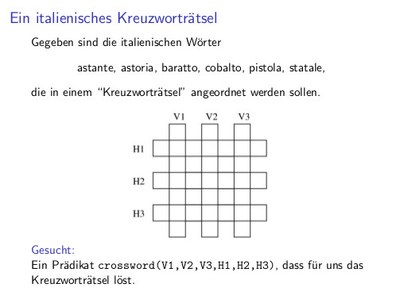
Aufgabe 2.4 aus [BBS]
Die Worte werden dabei wie folgt in der Wissensbasis repräsentiert:
word(astoria, a,s,t,o,r,i,a).
word(baratto, b,a,r,a,t,t,o).
word(cobalto, c,o,b,a,l,t,o).
word(pistola, p,i,s,t,o,l,a).
word(statale, s,t,a,t,a,l,e).
Programmieren mit Nicht-Unifizierbarkeit:
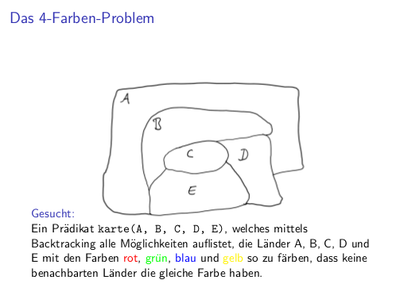
Woche 03
kind(brigitte, carolin).
kind(carolin, donna).
kind(donna, emilie).
nachkomme(X, Y) :- kind(X, Y).
nachkomme(X, Y) :- kind(X, Z), nachkomme(Z, Y).
kind(brigitte, carolin).
kind(carolin, donna).
kind(donna, emilie).
nachkomme(X, Y) :- kind(X, Z), nachkomme(Z, Y).
nachkomme(X, Y) :- kind(X, Y).
kind(brigitte, carolin).
kind(carolin, donna).
kind(donna, emilie).
nachkomme(X, Y) :- nachkomme(Z, Y), kind(X, Z).
nachkomme(X, Y) :- kind(X, Y).
kind(brigitte, carolin).
kind(carolin, donna).
kind(donna, emilie).
nachkomme(X, Y) :- kind(X, Y).
nachkomme(X, Y) :- nachkomme(Z, Y), kind(X, Z).
numeral(succ(X)) :- numeral(X).
double(succ(X),succ(succ(Y))) :- double(X,Y).
add(0,Y,Y).
add(succ(X),Y,succ(Z)):- add(X,Y,Z).
greater(succ(_),0).
greater(succ(X),succ(Y)):-greater(X,Y).
offen:
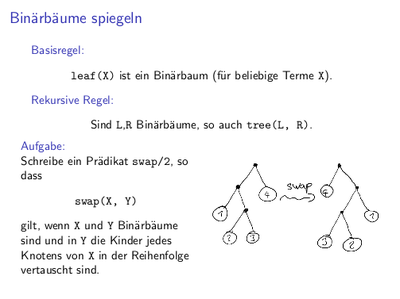
Woche 04
element(X,[_|T]) :- element(X,T).
invert([a|T1],[b|T2]) :- invert(T1,T2).
invert([b|T1],[a|T2]) :- invert(T1,T2).
evenElements([], []).
evenElements([_, X|T1], [X|T2]) :- evenElements(T1,T2).
Woche 05
laenge([_|T],L) :- laenge(T,LT),L is LT + 1.
laenge([_|T],A,N) :- AT is A + 1 , laenge(T,AT,N).
laenge(L, N) :- laenge(L,0,N).
prod([], A, A).
prod([H|T], A, P) :- A2 is A * H, prod(T, A2, P).
max([H|T], A, MT) :- H > A, max(T, H, MT).
max([H|T], A, MT) :- H =< A, max(T, A, MT).
max([H|T], M) :- max(T, H, M).
% CAKE
% STORY
ziffer(0).
ziffer(1).
ziffer(2). ziffer(3). ziffer(4). ziffer(5).
ziffer(6). ziffer(7). ziffer(8). ziffer(9).
raetsel(F, A, K, E, C , S, T, O, R,Y) :-
ziffer(F), ziffer(A), ziffer(K), ziffer(E),ziffer(C),
ziffer(S), ziffer(T), ziffer(O), ziffer(R), ziffer(Y),
F =\= A, F =\= K , F =\= E, F =\= C, F =\= S, F =\= T, F =\= O, F =\= R, F =\= Y,
A =\= K , A =\=E, A =\=C, A =\=S, A =\=T, A =\=O, A =\=R, A =\=Y,
K =\=E, K =\=C, K =\=S, K =\=T, K =\=O, K =\=R, K =\=Y,
E =\=C, E =\=S, E =\=T, E =\=O, E =\=R, E =\=Y,
C =\=S, C =\=T, C =\=O, C =\=R, C =\=Y,
S =\=T, S =\=O, S =\=R, S =\=Y,
T =\=O, T =\=R, T =\=Y,
O =\=R, O =\=Y,
R =\=Y,
S =\= 0, C =\= 0, F =\= 0,
Y =:= (E + E) mod 10, U1 is (E + E) // 10,
R =:= (K + K + U1) mod 10, U2 is (K + K + U1) // 10,
O =:= (A + A + U2) mod 10, U3 is (A + A + U2) // 10,
T =:= (F + C + U3) mod 10, S =:= (F + C + U3) // 10.
% Try:
% ?- time(findall([F, A, K, E, C , S, T, O, R,Y],raetsel(F, A, K, E, C , S, T, O, R,Y),Z)).
% CAKE
% STORY
ziffer(0).
ziffer(1).
ziffer(2). ziffer(3). ziffer(4). ziffer(5).
ziffer(6). ziffer(7). ziffer(8). ziffer(9).
raetsel(F, A, K, E, C , S, T, O, R,Y) :-
ziffer(E),
Y is (E + E) mod 10, U1 is (E + E) // 10,
ziffer(K),
R is (K + K + U1) mod 10, U2 is (K + K + U1) // 10,
ziffer(A),
O is (A + A + U2) mod 10, U3 is (A + A + U2) // 10,
ziffer(F), ziffer(C),
T is (F + C + U3) mod 10, S is (F + C + U3) // 10,
F =\= A, F =\= K , F =\=E, F =\=C, F =\=S, F =\=T, F =\=O, F =\=R, F =\=Y,
A =\= K , A =\=E, A =\=C, A =\=S, A =\=T, A =\=O, A =\=R, A =\=Y,
K =\=E, K =\=C, K =\=S, K =\=T, K =\=O, K =\=R, K =\=Y,
E =\=C, E =\=S, E =\=T, E =\=O, E =\=R, E =\=Y,
C =\=S, C =\=T, C =\=O, C =\=R, C =\=Y,
S =\=T, S =\=O, S =\=R, S =\=Y,
T =\=O, T =\=R, T =\=Y,
O =\=R, O =\=Y,
R =\=Y,
S =\= 0, C =\= 0, F =\= 0.
% Try:
% ?- time(findall([F, A, K, E, C , S, T, O, R,Y],raetsel(F, A, K, E, C , S, T, O, R,Y),Z)).
Offen: Der Klassiker der Rekursion
Die Fakultät n! einer natürlichen Zahl n ist definiert durch:

Definieren Sie
- ein Prädikat fak/2, dass bei Anfrage fak(X,Y) die Fakultät von X mit Y unifiziert.
- ein Prädikat fakAcc/2, dass äquivalent zu fak/2 ist und "End-Rekursiv” realisiert.
Woche 06
verkettet([], Y, Y).
verkettet([H|T], Y, [H|T2]) :- verkettet(T, Y, T2).
% praefix
praefix(X, Y) :- verkettet(X, _, Y).
% suffix
suffix(X, Y) :- verkettet(_, X, Y).
umgedreht([], []).
umgedreht([H|T], R) :-
umgedreht(T, RT), verkettet(RT, [H], R).
% mit Akkumulator
umgedrehtAcc([], A, A).
umgedrehtAcc([H|T], A, R) :-
umgedrehtAcc(T, [H|A], R).
umgedrehtAcc(L, R) :- umgedrehtAcc(L, [], R).
% verkettet
verkettet([], Y, Y).
verkettet([H|T], Y, [H|T2]) :- verkettet(T, Y, T2).
not_member(X, [H|T]) :- X \= H, not_member(X, T).
atree(tree(L, R)) :- atree(L), atree(R).
sum_labels(tree(L, R), N) :-
sum_labels(L, NL), sum_labels(R, NR),
N is NL + NR.
Offen:
Definieren Sie ein Prädikat lookup/3, so dass lookup(X, L, Y) genau dann erfüllt ist, wenn L eine Liste von 2-Tupeln (A, B) ist, die insbesondere das Tupel (X, Y) enthält.
Beispielsweise sollte es folgene Ausgaben liefert:
X = 2 ;
false.
?- lookup(b, [(a, X), (b, Y), (c, Z)], 3).
Y = 3 ;
false.
node(f). node(g). node(h). node(i). node(j).
edge(a, j).
edge(c, e).
edge(d, e).
edge(e, f).
edge(f, g).
edge(g, h). edge(g, j).
edge(h, g). edge(h, i).
edge(i, a). edge(i, b). edge(i, j).
edge(j, b). edge(j, c). edge(j, d). edge(j, f).
erreichbar(X, X).
erreichbar(X, Y) :-
edge(X, Z), erreichbar(Z, Y).
% Try: ?- erreichbar(a, g).
% Try: ?- erreichbar(h, a).
node(f). node(g). node(h). node(i). node(j).
edge(a, j).
edge(c, e).
edge(d, e).
edge(e, f).
edge(f, g).
edge(g, h). edge(g, j).
edge(h, g). edge(h, i).
edge(i, a). edge(i, b). edge(i, j).
edge(j, b). edge(j, c). edge(j, d). edge(j, f).
erreichbarMem(X, Y) :- erreichbar(X, Y, [X]).
erreichbar(X, X, _) .
erreichbar(X, Y, Pfad) :-
edge(X, Z), not_member(Z, Pfad),
erreichbar(Z, Y, [Z|Pfad]).
% Try: ?- erreichbarMem(a, g).
% Try: ?- erreichbarMem(h, a).
% not_member
not_member(_, []).
not_member(X, [H|T]) :- X \= H, not_member(X, T).
Woche 07
distribute((A + B)*C, A*C + B*C).
numbers(L + R, X) :-
numbers(L, XL), numbers(R, XR),
append(XL, XR, X).
numbers(L * R, X) :-
numbers(L, XL), numbers(R, XR),
append(XL, XR, X).
atom_codes(N, SN),
atom_codes("x", XN),
append(XN, SN, S),
atom_codes(A, S).
Literatur
| [BBS] | Patrick Blackburn, Johan Bos, Kristina Striegnitz, Learn PROLOG Now!. Kings College Publications, 2006. Online version. |
| [SS] | Ehud Shapiro, Leon Sterling, The Art of PROLOG: Advanced Programming Techniques. 2nd Edition, MIT Press, 1994. |
Programmierressourcen
SWI-Prolog. Eine Kurzanleitung für den Einstieg in SWI-Prolog.
